تابعی است که هم دامنه تعریف آن و هم مقدار آن هردو مختلط باشند. به این ترتیب، یک تابع مختلط، تابعی از فضای به فضای میباشد.
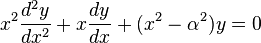
که α یک عدد حقیقی یا مختلط دلخواه میباشد که مرتبه تابع بسل را مشخص میکند. بطورکلی توابع بسل از حل معادلات دیفرانسیل پارهای لاپلاس ( Laplace's equation) و هلمهلتز (Helmholtz equation) در مختصات استوانهای و مختصات کروی بدست میآیند. از این رو این توابع در تیوری انتشار امواج و تیوری پتانسیل اهمیت بسزایی دارند. البته این توابع در حل معادلات ارتعاشات، معادلات رسانایی گرما و امواج الکترومغناطیس در مختصات استوانهای ظاهر میشوند.
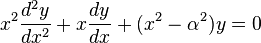
جوهر ریاضی درآزادی آن نهفته است.